안녕 게이들아?
이번에는 좀 최신의 곱셈 알고리즘에 대해 알아보려고 해.
아르놀드 쇤하게(Arnold Schoenhage)와 폴커 슈트라센(Volker Strassen)이 1971년에 개발한 Schönhage–Strassen algorithm에 대해 알아보려고해.
그런데 이 알고리즘은 FFT를 이용해서 곱셈하는 것을 더욱 효율적으로 개량한 것인데, 문과 일게이나 수학과 별로 친하지 않은 일게이들은 FFT가 뭔지도 모르는 경우가 대부분일거야.
그래서 1편에서는 FFT를 이용해서 곱셈을 하는 법을 위주로 알아보고, 2편에서 본격적인 쇤하게-슈트라센 알고리즘을 알아볼거야.
1. FFT란 무엇인가?
먼저 이 곱셈법의 핵심은 FFT를 이용하는 거야.
근데 FFT를 처음 듣는 게이들도 있을 텐데 설명을 안해주면 곱셈을 할 수가 없겠지?
FFT는 Fast Fourier transform의 약자야.
한글로는 고속 푸리에 변환이라고도 하는데, 말그대로 푸리에 변환을 빠르게 해주는 것이야.
정확하게 말하면 이산 푸리에 변환(Discrete Fourier transform)을 빠르게 처리해주는 알고리즘이야.
그럼 푸리에 변환이 뭔지 또 알아야겠지?
푸리에 변환은 어떤 함수가 있으면 이를 주파수 영역에 대한 함수로 바꿔주는 변환이야.
어떤 시간에 따라 함수값이 계속 변하는 입력을 받으면, 푸리에 변환을 통해 주파수에 따른 함수로 바꿔주는 거지.
그리고 이산 푸리에 변환은 연속적인 데이터가 아닌 이산적인 (떨어져있는) 자료들을 바탕으로 주파수를 함수로 바꿔주는 변환이야.
일반적으로 복소수를 입력으로 받아서 처리해.
그냥 푸리에 변환은 연속적인 입력을 받기 때문에 몇 개인지 알 수 없지만, 이산 푸리에 변환은 이산적인 입력을 받기 때문에 몇 개라고 셀 수 있어.
아.. 푸리에 변환은 뭐고 이산 푸리에 변환은 뭐고 또 복소수는 뭐노?
이번 글에서 이런 건 다 필요 없어.
우린 복소수를 다룰 것이 아니기 때문이지.
그렇다면 우리가 다룰 FFT는?
우리가 다룰 FFT는 디스크릿 푸리에 트랜스폼을 빠르게 한 것이긴 한데, 입력으로 받을 애들이 복소수가 아니라 정수야.
그리고 푸리에 트랜스폼은 원래 복소수를 오일러 공식으로 표현하면 주기성을 가진다는 것을 이용해서 뭔가를 하는 것인데,
정수도 똑같이 주기성을 갖도록 만들어 주면 돼.
어떻게?
그건 아래에서 설명하도록 하고, 이해를 돕기 위해 예시를 살펴보자.
x가 입력으로 받을 수들이야.
예를 들기 위해 x0=0, x1=1, x2=2, x3=3으로 생각하자.
W는 주기성을 갖는 수야.
이 예시에서는 10으로 둘거야.
10의 거듭제곱이 주기성을 갖냐고? 이건 이따가 말해줄게.
n은 자료의 수야.
x0~x3까지 있으니 총 4개의 자료가 있지?
n=4야.
이 때, xj의 푸리에 트랜스폼을 fj라고 하면,
다음과 같은 식에 의해 정의가 돼.

<수식1>
좀 복잡해 보이지?
하지만 정의니까 군말없이 외워야해..
이를 복잡하긴 마찬가지지만 행렬의 모양으로 보자.

<수식2>
한결 낫나?
이제 이것을 계산해보자.

<수식3>
이런식으로 계산해주면 돼.
근데 노무노무 복잡하지 않냐고?
그래서 이제 10의 주기성을 이용할거야.
이 때 키는 101야.
101가 뭔 소리냐 하면, 각 값들을 101로 나눈 나머지만 쓰겠다. 이기야.
이렇게 되면 10^4=1 (mod 101)이 돼.
10을 4제곱하면 10000이지? 이걸 101로 나누면 10000-9999=1 나머지가 1이 돼.
이제 주기성이 생겼지?
이 단락에서 모든 수들은 mod 101로 생각할거야.
W0=1
W1=10
W2=100=-1
W3=91=-10
그럼 f0~f3을 다시 구해보자.

<수식4>
호옹이?
한결 간단해진 느낌이 들지 않노?
그리고 보면 f1같은 경우는 -22가 나와서 매우 찝찝할 수도 있다.
하지만 여기에 101을 더해준 79나 -22나 같은 것이기 때문에 전혀 문제가 없다.
나중에 모든 계산이 끝나고 그냥 +101 해주면 된다.
아까 f1을 3210으로 구했을 때나 –22나 79나 mod 101에서는 모두 같다.
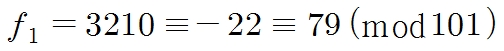
<수식5>
(작대기가 3개 있는 기호는 합동식기호로, 이 경우에는 두 수가 101로 나눈 나머지가 같다는 것을 의미하고 있다.)
3210에서 3232를 빼주면 알 수 있다.
2. FFT 알고리즘
이제 우리가 알아볼 것은 FFT 알고리즘이다.
사실, 그냥 푸리에 트랜스폼을 계산할 때는
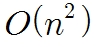
만큼의 복잡도가 필요하다.
이게 뭔 개소리냐 하면, 1에서 우리가 예시로 4*4짜리 행렬로 계산을 했다.
즉, n=4인 경우인데 이 때 우리는 총 16번의 곱셈을 수행했다.
하지만 FFT를 사용하면 이 시간 복잡도가

으로 줄어들게 된다.
간단한 예를 들어보면, 1000*1000짜리 계산을 하려면 그냥 푸리에 트랜스폼으로는 1,000,000회의 곱셈이 필요하지만, FFT를 이용하면 1000*3=3,000회의 곱셈만으로도 푸리에 트랜스폼을 할 수 있다는 이야기다.
이것이 어떻게 가능하느냐?
이와 관련된 여러 가지 알고리즘들이 있지만, 그 중에서 가장 대표적이고 이해하기 쉬운 알고리즘인 쿨리-투키(Cooley=Tukey)알고리즘만을 간단히 알아볼 계획이야.

<수식2>
이게 원래 우리가 알고 있던 푸리에 트랜스폼의 매트릭스 모양이지?
여기서 왼쪽 행렬의 2,3열을 바꿔준다. 왼쪽 행렬의 2,3열을 바꿔줬기 때문에 equivalent한 연산이 되려면 오른쪽 행렬의 2,3행도 바꿔줘야한다. (x1와 x2의 위치를 바꿈)

<수식6>
그러면 결과적으로 위의 중간에 있는 꼴로 바뀌게 된다. 여기서 W^4=1을 이용하고 곱해진 인수들을 분해하면 오른쪽 같은 꼴로 바뀌게 된다.
이제 오른쪽에 있는 계산을 아래와 같이 분리 해낼 수 있다.

<수식7>
이제 우리는 4*4짜리 푸리에 트랜스폼을 8회의 곱셈만으로 구하게 된 것이다.
셈이 빠른 게이들은 위의 행렬에는 분명히 왼쪽에 변수4개, 중앙에 변수 8개, 오른쪽에 변수 4개가 있으니 총 4*8=32회의 계산이 필요한 게 아닌가 하고 물을 수도 있다.
하지만 위의 공식은 사실 아래와 같이 계산된다.

<수식8>
W_2 = W^2 이다.
W는 n=4의 W이고
W_2는 n=2의 W를 의미한다.
아무튼 그렇게 해서 저 식을 살펴보면 차례대로 계산하다 보면 t들을 계산할 때 각각 곱셈 1번, 최종적으로 f를 계산할 때 곱셈 1번이 이루어져 총 8회의 곱셈만으로 계산이 끝난다는 것을 알 수 있다.
여기서 어떤 게이는 다음과 같이 질문할 수 있다.
“W^2는 W*W니까 곱셈 횟수에 카운트 해야하는 것 아니냐?”
FFT의 행렬을 구하는 것은 미리 계산하여 입력이 가능하므로 상수 취급한다.
즉, FFT를 이용하면(특히 쿨리-투키 알고리즘) n=2^k의 크기의 푸리에 트랜스폼을 k*n 회의 곱셈만에 처리할 수 있다는 사실을 알았다.
그리고 위에서는 x1과 x2의 위치를 바꾸는 정도로만 말했는데, 만약 x가 더 커질 경우에는 x부분을 정확히 반으로 쪼개서 윗부분은 짝수(0,2,4,8,..) 아랫부분은 홀수(1,3,5,7,...)로 두면 된다.
3. 곱셈과의 관계
지금까지 푸리에 트랜스폼과 FFT에 대해 설명을 했는데, 이제 가장 중요한 부분이다.
“그래서 정수곱셈이랑 무 슨상 관?”
우리가 1234와 5678을 곱한다고 해보자.
일단 우리는 다음과 같이 곱셈을 할 수도 있을 것이다.

<그림1>
더했을 때 10의 자리가 생기는 것을 고려하지 않고, 일단 같은 자리들 끼리만 더한 값들을 구한다.

<그림2>
그리고 이렇게 더해준다.
그러면 결과인 7006652가 나오게 된다.
이 식을 본 게이들은 화가 날 것이다.
“엥? 저거 완전 그냥 곱셈법이잖아!”
맞다. 저건 그냥 곱셈법이다.
FFT를 이용하여 time complexity를 줄이는 부분은 바로 5,16,34,60,61,52,32와 같은 같은 자리수의 합을 구하는 과정이다.
아까 10이 주기성을 갖는다고 했지?
보통의 정수 연산에서는 10의 거듭제곱은 주기성을 갖지 않는다.
10, 100, 1000, 10000, ... 이런 식으로 계속 증가하는 형태를 보일 뿐이다.
하지만 modulo-101의 ring에서는 다르다.
(modulo-N의 ring은 0~(N-1)까지의 정수들로만 이루어진 수 집합에서 덧셈, 곱셈이 정의된 것을 의미한다.)
10, 100(=-1), 1000(=91=-10), 10000(=1), ...
이렇게 10의 거듭제곱은 10, -1, -10, 1을 반복한다.
이러한 ring을 만들기 위해서는 먼저 적당한 N과 W를 찾아야 한다.
이번 글에서는 우리는 모두 10진수를 기준으로 이야기를 할 것이다.
N과 W의 조건
1. N은 81*n보다 커야 한다.
여기서 말하는 n은 숫자의 자리수이다. 만약 1234*5678을 계산한다고 하면, N은 최소 81*n보다는 커야 한다.
왜냐하면 우리는 최소 81*n개 이상의 서로 다른 숫자들이 필요하기 때문이다.
위의 1234*5678을 구하는 식에서 1234의 1, 5678의 5가 있는 밑에 줄의 4개의 숫자들을 보자.
만약 9999*9999을 구하는 과정이라면 어떻게 될까?
4개의 81이 더해질 것이다.
따라서 B진법에서 두 n자리 수의 곱셈을 할 때는 n(B-1)^2보다 큰 수로 N을 잡아야 한다.
2. <수식9>를 만족한다.

<수식9>
(합동기호에 not이 붙은 기호를 찾지 못해서 그냥 not equal로 표기했다. 양해 바람)
W을 n번 곱했을 때 1이 되어야 한다. 대신 n보다 작은 수 k에 대해서, W를 k번 곱한 값이 1이 되면 안된다.
이 두 조건을 만족해야 하기 때문에, N=101은 부적절하다.
하지만 우리가 볼 예시는 곱의 합이 101을 넘지 않는 2자리 수의 곱셈이므로 N=101을 이용해도 된다.
3. <수식10>을 만족하는 x가 존재해야 한다.

<수식10>
이게 뭔 소린고 하니 역변환할 때 x의 역원이 필요하다. 그런데 역원이 존재하지 않는다면 곱셈을 구할 수 없다.
만약 N=101, n=4라면 x=76과 같은 수가 반드시 존재해야 한다는 것이다.
자, N과 W를 결정하는 조건은 이제 알았으니 본격적으로 곱셈과 무현슨상관인지를 알아보자.
합성곱(convolution)이라는 개념이 있다. 솔직히 말하면 이것의 원래 개념이 정확하게 무엇인지는 모른다.
하지만 이산적인 함수에 대해서는 합성곱을 다음과 같이 정의한다.

<수식11>
별표(asterisk)로 표시한 것이 합성곱의 기호이다.
f와 g를 각 자리를 나타내는 함수라고 하자.
그러면 f*g는 위의 1234*5678의 경우에서 (5, 16, 34, 60, 61, 52, 32)를 의미할 것이다.
(사실 순서는 반대로다. (f*g)(0)=32이다)
우변의 의미도 정확히 이것과 같다.
총 n은 0부터 m까지 갈 것이다.
f(n)과 g(n)을 각각 곱할 두 수의 n번째 자리를 나타내는 함수라고 하면,
(f*g)(m)=f(0)g(m)+f(1)g(m-1)+...+f(m-1)g(1)+f(m)g(0) 이다.
0번째부터 m번째 자리 까지 수들을 차례대로 교차해가며 다 곱한 값들을 더한 값이다.
합성곱 정리라는 것이 있다.

<수식12>
F에 끝이 약간 이상하게 생긴 저 문자는 푸리에 트랜스폼을 의미한다.
두 함수를 합성곱한 것을 푸리에 트랜스폼 한 것은, 각 각의 함수를 푸리에 트랜스폼해서 점별 곱셈(각 점끼리 곱한 값을 모아 놓은 것)과 같다는 정리이다.
이 때, 푸리에 트랜스폼의 역변환도 있다. 양변에 역변환을 취해주면 우리가 원하는 f*g값을 얻을 수 있는 것이다.

<수식13>
호옹이.. 근데 푸리에 역변환은 어떻게 구하노?

<수식14>
이렇게 하면 된다.
참 쉽지?
이것의 FFT는 위의 정변환의 FFT를 하는 법과 같다.
행렬도 그대로 쓰면 되는데 대신 각 숫자들의 역수를 구해야 한다.
그것 말고는 n=4기준으로 볼 때 f1와 f2의 위치를 바꿔주면 된다.
(정확히는 절반으로 나눠서 윗부분은 짝수번째 값들이 오게, 아랫부분은 홀수번째 값들이 오도록)
그 외에 정변환 행렬과 다른 점은 앞에 1/N이 있다는 점이다.
그런데.. 앞에서 말한 거 기억나노?
우리는 “정수”들만 쓰기로 했다.
즉, 1/N 같은 건 없다 이기다.
마찬가지로 행렬을 쓸 때 “역수“를 쓰라는 건 분자와 분모를 뒤집는 그런 역수를 말하는 것이 아니다.
만약 10이란 숫자가 있던 자리가 있으면 1/10을 쓰라는 말이 아니라는 것이다.
그렇다면 역수를 어떻게 구하느냐?
일반적인 수 체계에서 곱셈의 역원을 구해보자.

<수식15>
y는 x의 역수이다.
이제 우리의 수체계로 돌아와보자. 이도 마찬가지이다.

<수식16>
y는 x의 역수이다.
즉, 두 수를 곱해서 N으로 나눈 나머지가 1이 되면 되는 것이다.
이러한 방식으로 각 자리의 수의 역수를 취해준다.
역변환 행렬의 앞의 1/n도 마찬가지다.
우리의 경우는 n=4였고 N=101이었으니까, 4n을 101로 나눴을 때 나머지가 1이 되는 n을 구하면 된다.
계산해보면 76이 나온다.
즉, 1/n=76인 것이다.
이제 곱셈을 위한 준비는 모두 끝났다.
FFT를 이용하여 곱셈을 하기 위해서는 다음과 같은 절차를 거치면 된다.
곱하고 싶은 두 수를 정한다. (두 수를 a,b라고 하자)
조건에 만족하는 N과 W찾는다.
a의 FFT를 취한다.
b의 FFT를 취한다.
FFT 취한 것을 점끼리 곱한다.
곱한 것에 FFT의 역변환을 취한다.
자리수에 맞춰서 더한다.
참 간단해 보이지 않노?
4. 예제
어떻게 하는 지 배웠으니 이제 우리가 직접 계산해보자 이기야!
1. 곱하고 싶은 두 수는 12와 34이다.
2. N은 101과 W는 10이다.
(일반적으로 두 수를 곱할 때는 최소 182가 넘는 수를 사용해야 하지만, 1,2,3,4는 아무리 곱해서 더해봤자 81도 못 넘으므로 101을 해도 충분하다.)
3. 12의 FFT를 구한다.
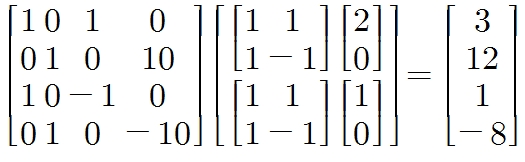
<수식17>
4. 34의 FFT를 구한다.

<수식18>
5. 각 entry 끼리 곱한다.

<수식19>
6. 5의 FFT 역변환을 구한다.

<수식20>
7. 자리수에 맞춰서 더한다.
8*1+10*10+3*100=408
어떻노?
노무노무 쉽지 않노?
5번 과정에서 원래 우리의 목표인 12*34를 구해야 하는 걸 보고 노무노무 빡친 게이도 있을 거야.
하지만 그건 예시로 든 숫자가 노무 작아서 그렇다.
하나 만 더 해보자.
1. 곱하고 싶은 두 수는 1234와 5678이다.
2. N=337, W=85이다. (81*4=324니까 최소 324보다는 커야하고 나머지 조건도 만족해야 한다.)
3. 1234를 FFT한다.

<수식21>
4. 5678을 FFT한다.

<수식22>
5. 각 entry끼리 곱한다.

<수식23>
6. 5의 역 FFT를 구한다.

<수식24>
7. 자리수에 맞춰서 더한다.

<그림2>
2번째 예제도 사실은 기존 방법보다 더 많은 시간이 든다.
그렇다면 이 알고리즘은 후진걸까?
5. 효율성 검증
한자리 곱셈에만 초점을 두고 따져보자. (덧셈, 나머지 연산 등은 무시)
n자리 수를 계산할 때, 기존의 방법으로 하면 곱셈이 n^2 만큼 필요하다.
그렇다면 FFT를 이용한 방법은?
n=2^k라고 두면,
2n(=2^(k+1))자리의 FFT가 필요하기 때문에 FFT 한번당 (k+1)*2*(2^k) 회의 곱셈이 필요하다.
그런데 정변환 2번, 역변환 1번을 했기 때문에 총 3회의 FFT 계산이 필요하다.
그리고 점별 계산 과정에서 2^k 만큼의 곱셈을 했다.
따라서 총 필요한 곱셈 횟수는 (6k+7)*(2^k) 회의 곱셈횟수가 필요하다.
그리고 하나 더.
각각의 곱셈은 사실 1자리 곱셈이 아니다.
예제 2번 같은 경우에는 N이 세자리여서 최대 9번의 계산을 했었다.
N의 자릿수에 따라 또한 곱셈횟수가 증가한다.
N의 자릿수를 구하자.
logN=log(n*81)=logn+log81=klog2+log81
최악의 경우 N^2를 계산해야하므로 (klog2+4log3)^2 만큼의 계산이 필요하다.
따라서 FFT를 이용하여 곱셈을 하는 경우에 (klog2+4log3)^2*(6k+7)*(2^k) 만큼의 곱셈이 필요하다.
반면 고전 방식은? 그냥 (2^k)*(2^k) 만큼의 시간만 필요하다.
이것을 직접 계산을 통해 언제부터 FFT가 유리한 지 알아보자.
이 식에 의해서 구한 복잡도 그래프이다.

<그림3>

<그림4>
대략적으로 2~3천자리 쯤에서 FFT가 고전방식의 속도를 역전한다.
또한 1자리~4억자리를 비교해볼 때, 고전방식으로 계산했을 때를 1로 뒀을 때, 숫자가 커지면 커질수록 FFT로 곱셈을 연산할 경우 엄청난 시간을 절약할 수 있음을 알 수 있다.
아까 n=2^k일 때, 소요되는 시간은 (klog2+4log3)^2*(6k+7)*(2^k) 라고 했었는데
이를 Big Oh Notation으로 표시하면,

이다.
그런데 쇤하게-슈트라센 알고리즘은

이다.
도대체 무슨 짓을 했길래 저만큼의 시간이 줄어들었는 지는 2편에서..
원글














